Characteristics of Sound and the Decibel Scale

There are two important characteristics of sound or noise - frequency and loudness.

Frequency of Sound

Sound is the quickly varying pressure wave travelling through a medium. When sound travels through air, the atmospheric pressure varies periodically. The number of pressure variations per second is called the frequency of sound, and is measured in Hertz (Hz) which is defined as cycles per second.

The higher the frequency, the more high-pitched a sound is perceived. The sounds produced by drums have much lower frequencies than those produced by a whistle, as shown in the following diagrams. Please click on the demo button to hear their sounds and the difference in pitch.

Loudness and the Decibel Scale

Another property of sound or noise is its loudness. A loud noise usually has a larger pressure variation and a weak one has smaller pressure variation. Pressure and pressure variations are expressed in Pascal, abbreviated as Pa, which is defined as N/m²(Newton per square metre).

Human ear can perceive a very wide range of sound pressure. The softest sound a normal human ear can detect has a pressure variation of 20 micro Pascals, abbreviated as µPa, which is 20 x 10^-6 Pa ("20 millionth of a Pascal") and is called the Threshold of Hearing. On the other hand, the sound pressure close to some very noisy events such as launching of the space shuttle can produce a large pressure variation at a short distance of approximately 2000 Pa or 2 x 10⁹ µPa. The following table illustrates sound pressure level of the above events expressed in Pa and µPa.

	Sound Pressure expressed in
	Pa	µPa
Softest Noise just Heard by a Human Ear	20 x 10^-6	20
Launching of the Space Shuttle	2,000	2 x 10⁹

To express sound or noise in terms of Pa is quite inconvenient because we have to deal with numbers from as small as 20 to as big as 2,000,000,000.

The following table shows some common sound or noise in terms of µPa:

Source of Sound/Noise	Approximate Sound Pressure in µPa
Launching of the Space Shuttle	2,000,000,000
Full Symphony Orchestra	2,000,000
Diesel Freight Train at High Speed at 25 m	200,000
Normal Conversation	20,000
Soft Whispering at 2 m in Library	2,000
Unoccupied Broadcast Studio	200
Softest Sound Human can Hear	20

A simpler way is to use a logarithmic scale for the loudness of sound or noise, using 10 as the base. The following is a brief introduction of the common logarithm to the base 10.

Click on the demo button, you may learn more about the relationship between linear and logarithmic scales.

To avoid expressing sound or noise in terms of Pa, which could involve some unmanageable numbers, the decibel or dB scale is used. The scale uses the hearing threshold of 20 μPa or 20 x 10^-6 Pa as the reference level. This is defined as 0 dB.

Sound pressure level, which is often abbreviated as SPL or L_p, in decibels (dB), can then be obtained using the following formula. You can click on the demo button to learn the formula.

In the following chart, some sounds are expressed both linearly in µPa and logarithmically in dB. One can see how the logarithmic scale helps us to handle numbers on a wide scale much more easily.

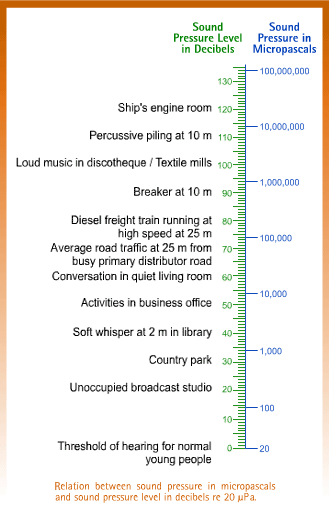
Chart illustrates relation between sound pressure in micropascal and decibel

One useful aspect of the decibel scale is that it gives a much better approximation to the human perception of relative loudness than the Pascal scale. This is because human ear responds to the logarithmic change in level, which corresponds to the decibel scale.

Adding Sounds or Noises together on the Decibel Scale

In real life, several sources of sounds often occur at the same time. One may be interested to know what results when one sound is combined with another, i.e. the addition of sounds.

Adding 60 apples to 60 apples results in 120 apples. But this is not the case with sounds when they are expressed in decibels. In fact, adding 60 decibels to 60 decibels gives 63 decibels. The following formula explains the general principle of adding sounds on the decibel scale. Please click on the demo button to see the details.

One can use the above formula to add three sounds together - 60 dB, 65 dB and 70 dB. Please click on the demo button to learn how to use the formula to add the three sounds together.

Addition of sound levels can also be done simply using the following chart.

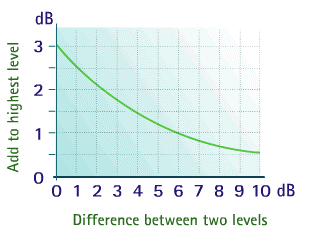
Chart for adding sound or noise

Let us try adding the three sounds of 60 dB, 65 dB and 70 dB by using the chart.

In using the Chart, two sounds are added together first. The resultant sound is then added to a third sound and so on. Please click on the demo button to understand how to add the SPL₁, SPL₂ and SPL₃ together.

Click on the demo button, you can learn how to add the sound levels using the chart.

The "A-weighting"

A normal human ear is able to hear sounds with frequencies from 20 Hz to 20,000 Hz. The range of 20 Hz to 20,000 Hz is called the audible frequency range. The sounds we hear comprise of various frequencies. The entire audible frequency range can be divided into 8 or 24 frequency bands known as octave bands or 1/3 octave bands respectively for analysis. A particular sound or noise can be seen to be having different strengths or sound pressure levels in the frequency bands, as illustrated by the following diagram. Please click on the demo button to view how sounds can be divided into 8 octave bands and 24 1/3 octave bands.

One single sound pressure level is often used to describe a sound. This can be done by adding the contribution from all octave bands or 1/3 octave bands together to yield one single sound pressure level.

The response of the ear to sound is dependent on the frequency of the sound. The human ear has peak response around 2,500 to 3,000 Hz and has a relatively low response at low frequencies. Hence, the single sound pressure level obtained by simply adding the contribution from all octave bands or 1/3 octave bands together will not correlate well with the non-linear frequency response of the human ear.

This has led to the concept of weighting scales. The following diagram shows the "A-weighting" scale:

Chart of "A-weighting" scale

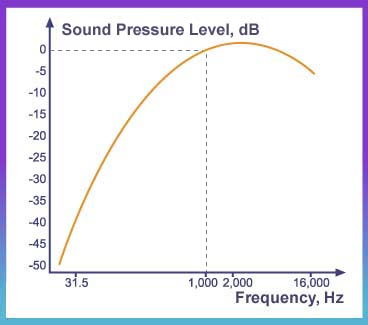
In the "A-weighting" scale, the sound pressure levels for the lower frequency bands and high frequency bands are reduced by certain amounts before they are being combined together to give one single sound pressure level value. This value is designated as dB(A). The dB(A) is often used as it reflects more accurately the frequency response of the human ear. Weighting networks are often incorporated in measuring equipments to give readings in dB(A).